This routine, along with spRoundoff(), are used to gauge the stability of a factorization. If the factorization is determined to be too unstable, then the matrix should be reordered. The routines compute quantities that are needed in the computation of a bound on the error attributed to any one element in the matrix during the factorization. In other words, there is a matrix 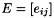 of error terms such that
of error terms such that 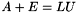 . This routine finds a bound on
. This routine finds a bound on 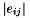 . Erisman & Reid [1] showed that
. Erisman & Reid [1] showed that 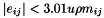 , where
, where 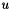 is the machine rounding unit,
is the machine rounding unit, 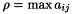 where the max is taken over every row
where the max is taken over every row 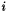 , column
, column  , and step
, and step 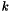 , and
, and 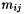 is the number of multiplications required in the computation of
is the number of multiplications required in the computation of 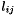 if
if 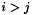 or
or 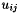 otherwise. Barlow [2] showed that
otherwise. Barlow [2] showed that 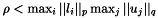 where
where 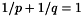 .
.
spLargestElement() finds the magnitude on the largest element in the matrix. If the matrix has not yet been factored, the largest element is found by direct search. If the matrix is factored, a bound on the largest element in any of the reduced submatrices is computed using Barlow with 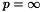 and
and 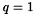 . The ratio of these two numbers is the growth, which can be used to determine if the pivoting order is adequate. A large growth implies that considerable error has been made in the factorization and that it is probably a good idea to reorder the matrix. If a large growth in encountered after using spFactor(), reconstruct the matrix and refactor using spOrderAndFactor(). If a large growth is encountered after using spOrderAndFactor(), refactor using spOrderAndFactor() with the pivot threshold increased, say to 0.1.
. The ratio of these two numbers is the growth, which can be used to determine if the pivoting order is adequate. A large growth implies that considerable error has been made in the factorization and that it is probably a good idea to reorder the matrix. If a large growth in encountered after using spFactor(), reconstruct the matrix and refactor using spOrderAndFactor(). If a large growth is encountered after using spOrderAndFactor(), refactor using spOrderAndFactor() with the pivot threshold increased, say to 0.1.
Using only the size of the matrix as an upper bound on 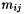 and Barlow's bound, the user can estimate the size of the matrix error terms
and Barlow's bound, the user can estimate the size of the matrix error terms 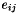 using the bound of Erisman and Reid. spRoundoff() computes a tighter bound (with more work) based on work by Gear [3],
using the bound of Erisman and Reid. spRoundoff() computes a tighter bound (with more work) based on work by Gear [3], 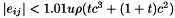 where
where 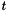 is the threshold and
is the threshold and 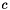 is the maximum number of off-diagonal elements in any row of
is the maximum number of off-diagonal elements in any row of 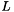 . The expensive part of computing this bound is determining the maximum number of off-diagonals in
. The expensive part of computing this bound is determining the maximum number of off-diagonals in 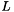 , which changes only when the order of the matrix changes. This number is computed and saved, and only recomputed if the matrix is reordered.
, which changes only when the order of the matrix changes. This number is computed and saved, and only recomputed if the matrix is reordered.
[1] A. M. Erisman, J. K. Reid. Monitoring the stability of the triangular factorization of a sparse matrix. Numerische Mathematik. Vol. 22, No. 3, 1974, pp 183-186.
[2] J. L. Barlow. A note on monitoring the stability of triangular decomposition of sparse matrices. "SIAM Journal of Scientific and Statistical Computing." Vol. 7, No. 1, January 1986, pp 166-168.
[3] I. S. Duff, A. M. Erisman, J. K. Reid. "Direct Methods for Sparse Matrices." Oxford 1986. pp 99.
- Returns :
- If matrix is not factored, returns the magnitude of the largest element in the matrix. If the matrix is factored, a bound on the magnitude of the largest element in any of the reduced submatrices is returned.
- Parameters:
-
eMatrix Pointer to the matrix.
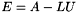 .
. 1.2.17
1.2.17