---

spConfig.h File Reference

#include <limits.h>
#include <float.h>

Go to the source code of this file.

Defines
#define	REAL   YES
#define	EXPANDABLE   YES
#define	TRANSLATE   YES
#define	INITIALIZE   YES
#define	DIAGONAL_PIVOTING   YES
#define	ARRAY_OFFSET   NOT FORTRAN
#define	MODIFIED_MARKOWITZ   NO
#define	DELETE   YES
#define	STRIP   YES
#define	MODIFIED_NODAL   YES
#define	QUAD_ELEMENT   YES
#define	TRANSPOSE   YES
#define	SCALING   YES
#define	DOCUMENTATION   YES
#define	MULTIPLICATION   YES
#define	DETERMINANT   YES
#define	STABILITY   YES
#define	CONDITION   YES
#define	PSEUDOCONDITION   YES
#define	FORTRAN   YES
#define	DEBUG   YES
#define	spCOMPLEX   1
#define	spSEPARATED_COMPLEX_VECTORS   0
#define	DEFAULT_THRESHOLD   1.0e-3
#define	DIAG_PIVOTING_AS_DEFAULT   YES
#define	SPACE_FOR_ELEMENTS   6
#define	SPACE_FOR_FILL_INS   4
#define	ELEMENTS_PER_ALLOCATION   31
#define	MINIMUM_ALLOCATED_SIZE   6
#define	EXPANSION_FACTOR   1.5
#define	MAX_MARKOWITZ_TIES   100
#define	TIES_MULTIPLIER   5
#define	DEFAULT_PARTITION   spAUTO_PARTITION
#define	PRINTER_WIDTH   80
#define	spcCONCAT(prefix, suffix)   prefix/**/suffix
#define	spcQUOTE(x)   "x"
#define	spcFUNC_NEEDS_FILE(func, file)   func/**/_requires_/**/file/**/_to_be_included_
#define	spcEXTERN   extern
#define	spcNO_ARGS
#define	spcCONST
#define	MACHINE_RESOLUTION   DBL_EPSILON
#define	LARGEST_REAL   DBL_MAX
#define	SMALLEST_REAL   DBL_MIN
#define	LARGEST_SHORT_INTEGER   SHRT_MAX
#define	LARGEST_LONG_INTEGER   LONG_MAX
#define	ANNOTATE   NONE
#define	NONE   0
#define	ON_STRANGE_BEHAVIOR   1
#define	FULL   2
Typedefs
typedef char *	spGenericPtr

---

Detailed Description

This file contains macros for the sparse matrix routines that are used to define the personality of the routines. The user is expected to modify this file to maximize the performance of the routines with his/her matrices.

Macros are distinguished by using solely capital letters in their identifiers. This contrasts with C defined identifiers which are strictly lower case, and program variable and procedure names which use both upper and lower case.

Objects that begin with the spc prefix are considered private and should not be used.

Author:

Kenneth S. Kundert <kundert@users.sourceforge.net>

---

Define Documentation

#define ANNOTATE   NONE

This macro changes the amount of annotation produced by the matrix routines. The annotation is used as a debugging aid. Change the number associated with ANNOTATE to change the amount of annotation produced by the program. Possible values include NONE, ON_STRANGE_BEHAVIOR, and FULL. NONE is recommended.

#define ARRAY_OFFSET   NOT FORTRAN

This determines whether arrays start at an index of zero or one. This option is necessitated by the fact that standard C convention dictates that arrays begin with an index of zero but the standard mathematic convention states that arrays begin with an index of one. So if you prefer to start your arrays with zero, or your calling Sparse from FORTRAN, set ARRAY_OFFSET to NO or 0. Otherwise, set ARRAY_OFFSET to YES or 1. Note that if you use an offset of one, the arrays that you pass to Sparse must have an allocated length of one plus the size of the matrix. ARRAY_OFFSET must be either 0 or 1, no other offsets are valid.

#define CONDITION   YES

This specifies that spCondition() and spNorm(), the code that computes a good estimate of the condition number of the matrix, should be compiled. Recomend NO.

#define DEBUG   YES

This specifies that additional error checking will be compiled. The type of error checked are those that are common when the matrix routines are first integrated into a user's program. Once the routines have been integrated in and are running smoothly, this option should be turned off. YES is recommended.

#define DEFAULT_PARTITION   spAUTO_PARTITION

Which partition mode is used by spPartition() as default. Possibilities include spDIRECT_PARTITION (each row used direct addressing, best for a few relatively dense matrices), spINDIRECT_PARTITION (each row used indirect addressing, best for a few very sparse matrices), and spAUTO_PARTITION (direct or indirect addressing is chosen on a row-by-row basis, carries a large overhead, but speeds up both dense and sparse matrices, best if there is a large number of matrices that can use the same ordering.

#define DEFAULT_THRESHOLD   1.0e-3

The relative threshold used if the user enters an invalid threshold. Also the threshold used by spFactor() when calling spOrderAndFactor(). The default threshold should not be less than or equal to zero nor larger than one. 0.001 is recommended.

#define DELETE   YES

This specifies that the spDeleteRowAndCol() routine should be compiled. Note that for this routine to be compiled, both DELETE and TRANSLATE should be set true.

#define DETERMINANT   YES

This specifies that the routine spDeterminant() should be complied.

#define DIAG_PIVOTING_AS_DEFAULT   YES

This indicates whether spOrderAndFactor() should use diagonal pivoting as default. This issue only arises when spOrderAndFactor() is called from spFactor(). YES is recommended.

#define DIAGONAL_PIVOTING   YES

Many matrices, and in particular node- and modified-node admittance matrices, tend to be nearly symmetric and nearly diagonally dominant. For these matrices, it is a good idea to select pivots from the diagonal. With this option enabled, this is exactly what happens, though if no satisfactory pivot can be found on the diagonal, an off-diagonal pivot will be used. If this option is disabled, Sparse does not preferentially search the diagonal. Because of this, Sparse has a wider variety of pivot candidates available, and so presumably fewer fill-ins will be created. However, the initial pivot selection process will take considerably longer. If working with node admittance matrices, or other matrices with a strong diagonal, it is probably best to use DIAGONAL_PIVOTING for two reasons. First, accuracy will be better because pivots will be chosen from the large diagonal elements, thus reducing the chance of growth. Second, a near optimal ordering will be chosen quickly. If the class of matrices you are working with does not have a strong diagonal, do not use DIAGONAL_PIVOTING, but consider using a larger threshold. When DIAGONAL_PIVOTING is turned off, the following options and constants are not used: MODIFIED_MARKOWITZ, MAX_MARKOWITZ_TIES, and TIES_MULTIPLIER.

#define DOCUMENTATION   YES

This specifies that routines that are used to document the matrix, such as spPrint() and spFileMatrix(), should be compiled.

#define ELEMENTS_PER_ALLOCATION   31

The number of matrix elements requested from the malloc utility on each call to it. Setting this value greater than 1 reduces the amount of overhead spent in this system call. On a virtual memory machine, its good to allocate slightly less than a page worth of elements at a time (or some multiple thereof). 31 is recommended.

#define EXPANDABLE   YES

Setting this compiler flag true (1) makes the matrix expandable before it has been factored. If the matrix is expandable, then if an element is added that would be considered out of bounds in the current matrix, the size of the matrix is increased to hold that element. As a result, the size of the matrix need not be known before the matrix is built. The matrix can be allocated with size zero and expanded.

#define EXPANSION_FACTOR   1.5

The amount the allocated size of the matrix is increased when it is expanded.

#define FORTRAN   YES

This specifies that the FORTRAN interface routines should be compiled. When interfacing to FORTRAN programs, the ARRAY_OFFSET options should be set to NO.

#define FULL   2

A possible value for ANNOTATE. Enables full annotation.

#define INITIALIZE   YES

Causes the spInitialize(), spGetInitInfo(), and spInstallInitInfo() routines to be compiled. These routines allow the user to store and read one pointer in each nonzero element in the matrix. spInitialize() then calls a user specified function for each structural nonzero in the matrix, and includes this pointer as well as the external row and column numbers as arguments. This allows the user to write custom matrix initialization routines.

#define LARGEST_LONG_INTEGER   LONG_MAX

The largest possible value of longs.

#define LARGEST_REAL   DBL_MAX

The largest possible value of spREAL.

#define LARGEST_SHORT_INTEGER   SHRT_MAX

The largest possible value of shorts.

#define MACHINE_RESOLUTION   DBL_EPSILON

The resolution of spREAL.

#define MAX_MARKOWITZ_TIES   100

Some terminology should be defined. The Markowitz row count is the number of non-zero elements in a row excluding the one being considered as pivot. There is one Markowitz row count for every row. The Markowitz column is defined similarly for columns. The Markowitz product for an element is the product of its row and column counts. It is a measure of how much work would be required on the next step of the factorization if that element were chosen to be pivot. A small Markowitz product is desirable. This number is used for two slightly different things, both of which relate to the search for the best pivot. First, it is the maximum number of elements that are Markowitz tied that will be sifted through when trying to find the one that is numerically the best. Second, it creates an upper bound on how large a Markowitz product can be before it eliminates the possibility of early termination of the pivot search. In other words, if the product of the smallest Markowitz product yet found and TIES_MULTIPLIER is greater than MAX_MARKOWITZ_TIES, then no early termination takes place. Set MAX_MARKOWITZ_TIES to some small value if no early termination of the pivot search is desired. An array of RealNumbers is allocated of size MAX_MARKOWITZ_TIES so it must be positive and shouldn't be too large. Active when MODIFIED_MARKOWITZ is 1 (YES). 100 is recommended. See also: TIES_MULTIPLIER

#define MINIMUM_ALLOCATED_SIZE   6

The minimum allocated size of a matrix. Note that this does not limit the minimum size of a matrix. This just prevents having to resize a matrix many times if the matrix is expandable, large and allocated with an estimated size of zero. This number should not be less than one.

#define MODIFIED_MARKOWITZ   NO

This specifies that the modified Markowitz method of pivot selection is to be used. The modified Markowitz method differs from standard Markowitz in two ways. First, under modified Markowitz, the search for a pivot can be terminated early if a adequate (in terms of sparsity) pivot candidate is found. Thus, when using modified Markowitz, the initial factorization can be faster, but at the expense of a suboptimal pivoting order that may slow subsequent factorizations. The second difference is in the way modified Markowitz breaks Markowitz ties. When two or more elements are pivot candidates and they all have the same Markowitz product, then the tie is broken by choosing the element that is best numerically. The numerically best element is the one with the largest ratio of its magnitude to the magnitude of the largest element in the same column, excluding itself. The modified Markowitz method results in marginally better accuracy. This option is most appropriate for use when working with very large matrices where the initial factor time represents an unacceptable burden. NO is recommended.

#define MODIFIED_NODAL   YES

This specifies that the routine that preorders modified node admittance matrices should be compiled. This routine results in greater speed and accuracy if used with this type of matrix.

#define MULTIPLICATION   YES

This specifies that routines that are used to multily the matrix by a vector, such as spMultiply() and spMultTransposed(), should be compiled.

#define NONE   0

A possible value for ANNOTATE. Disables all annotation.

#define ON_STRANGE_BEHAVIOR   1

A possible value for ANNOTATE. Causes annotation to be produce upon unusual occurances only.

#define PRINTER_WIDTH   80

The number of characters per page width. Set to 80 for terminal, 132 for line printer. Controls how many columns printed by spPrint() per page width.

#define PSEUDOCONDITION   YES

This specifies that spPseudoCondition(), the code that computes a crude and easily fooled indicator of ill-conditioning in the matrix, should be compiled. Recomend NO.

#define QUAD_ELEMENT   YES

This specifies that the routines that allow four related elements to be entered into the matrix at once should be compiled. These elements are usually related to an admittance. The routines affected by QUAD_ELEMENT are the spGetAdmittance(), spGetQuad() and spGetOnes() routines.

#define REAL   YES

This specifies that the routines are expected to handle real systems of equations. The routines can be compiled to handle both real and complex systems at the same time, but there is a slight speed and memory advantage if the routines are complied to handle only real systems of equations.

#define SCALING   YES

This specifies that the routine that performs scaling on the matrix should be complied. Scaling is not strongly supported. The routine to scale the matrix is provided, but no routines are provided to scale and descale the RHS and Solution vectors. It is suggested that if scaling is desired, it only be preformed when the pivot order is being chosen [in spOrderAndFactor()]. This is the only time scaling has an effect. The scaling may then either be removed from the solution by the user or the scaled factors may simply be thrown away. NO is recommended.

#define SMALLEST_REAL   DBL_MIN

The smalles possible positive value of spREAL.

#define SPACE_FOR_ELEMENTS   6

This number multiplied by the size of the matrix equals the number of elements for which memory is initially allocated in spCreate(). 6 is recommended.

#define SPACE_FOR_FILL_INS   4

This number multiplied by the size of the matrix equals the number of elements for which memory is initially allocated and specifically reserved for fill-ins in spCreate(). 4 is recommended.

#define spCOMPLEX   1

This specifies that the routines will be complied to handle complex systems of equations.

#define spSEPARATED_COMPLEX_VECTORS   0

This specifies the format for complex vectors. If this is set false then a complex vector is made up of one double sized array of RealNumber's in which the real and imaginary numbers are placed alternately in the array. In other words, the first entry would be Complex[1].Real, then comes Complex[1].Imag, then Complex[2].Real, etc. If spSEPARATED_COMPLEX_VECTORS is set true, then each complex vector is represented by two arrays of spREALs, one with the real terms, the other with the imaginary. NO is recommended.

#define STABILITY   YES

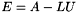This specifies that spLargestElement() and spRoundoff() should be compiled. These routines are used to check the stability (and hence the quality of the pivoting) of the factorization by computing a bound on the size of the element is the matrix . If this bound is very high after applying spOrderAndFactor(), then the pivot threshold should be raised. If the bound increases greatly after using spFactor(), then the matrix should probably be reordered. Recomend NO.

#define STRIP   YES

This specifies that the spStripFills() routine should be compiled.

#define TIES_MULTIPLIER   5

Specifies the number of Markowitz ties that are allowed to occur before the search for the pivot is terminated early. Set to some large value if no early termination of the pivot search is desired. This number is multiplied times the Markowitz product to determine how many ties are required for early termination. This means that more elements will be searched before early termination if a large number of fill-ins could be created by accepting what is currently considered the best choice for the pivot. Active when MODIFIED_MARKOWITZ is 1 (YES). Setting this number to zero effectively eliminates all pivoting, which should be avoided. This number must be positive. TIES_MULTIPLIER is also used when diagonal pivoting breaks down. 5 is recommended. See also: MAX_MARKOWITZ_TIES

#define TRANSLATE   YES

This option allows the set of external row and column numbers to be non-packed. In other words, the row and column numbers do not have to be contiguous. The priced paid for this flexibility is that when TRANSLATE is set true, the time required to initially build the matrix will be greater because the external row and column number must be translated into internal equivalents. This translation brings about other benefits though. First, the spGetElement() and spGetAdmittance() routines may be used after the matrix has been factored. Further, elements, and even rows and columns, may be added to the matrix, and row and columns may be deleted from the matrix, after it has been factored. Note that when the set of row and column number is not a packed set, neither are the RHS and Solution vectors. Thus the size of these vectors must be at least as large as the external size, which is the value of the largest given row or column numbers.

#define TRANSPOSE   YES

This specifies that the routines that solve the matrix as if it was transposed should be compiled. These routines are useful when performing sensitivity analysis using the adjoint method.

---